Starting today, I plan on focusing on the fundamental techniques of sound design. I won’t go too deep into the theory, as much of this information is described better elsewhere. My intent is to provide just enough of the basics so that you can start experimenting immediately, and hopefully start to recognize some of these synthesis design patterns as you study other instruments in the future. We begin with Ring Modulation.

The Computer Music Tutorial by Curtis Roads describes ring modulation as “simply the multiplication of two bipolar audio signals by one another.” Often times, one of the signals is a sine wave, though certainly not always. This technique is a quick and easy way for introducing inharmonic frequencies to a sound, and is quite popular in science fiction, as it is used in everything from 1950s era spaceships to robot voices. I’m personally fond of Daleks and Cybermen.

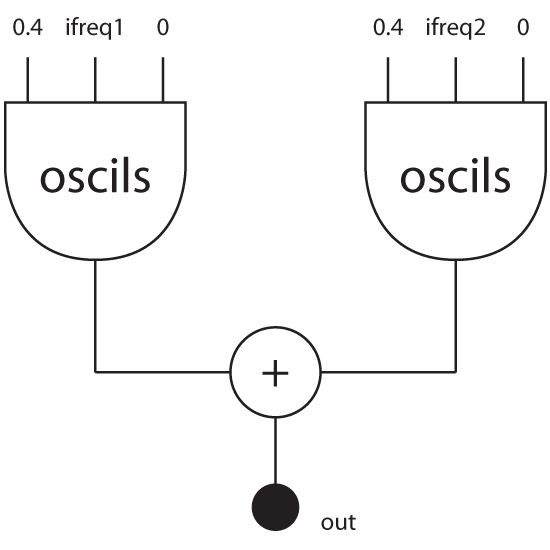
I created a simple example that ring modulates two sine wave oscillators together. The first oscillator has a constant frequency of 440Hz, while the second oscillator starts with a value of 1Hz, and doubles once a second until it plays the 2048Hz tone.

Download today’s example here.

Synthesis Fall 2010

Csound and other computer music languages are open ended, making room for users to approach a single problem or design choice in multiple ways. In the article Interfaces and Envelopes, three methods for generating multi-segment envelopes are discussed, explaining the pros and cons for each.

Synthesis Fall 2010

The first two weeks have been filled with perhaps too much information. Now is the perfect time to take a step back and really make sure the fundamentals are well covered, and properly understood.

To start, I’m presenting a simplified Csound example which contains lots of comments to help explain most of the things that are going on. I’ve also provided the block diagram above so you can get a sense of the signal flow of instr 1. Though I tried to be thorough, you should still have the Csound manual handy to help fill in anything missed.

If something doesn’t make sense, be sure you post a comment below, or send me an email.

Today’s example can be downloaded here.

Synthesis Fall 2010

Andrés Cabrera wrote an article for The Csound Journal called An Overview of Csound Variable Types. This is a great guide for demystifying that various signal types in Csound. There are siz types in all: audio (a), control (k), initialization (i), string (S), phase vocoder streaming (F) and spectral (w). Section II is especially useful as it provides various approaches for converting from one type to another, which you will find yourself doing from time to time.

Synthesis Fall 2010

As a general rule, Csound unit generators require that frequency is specified in terms of hertz, cycles per second. Though playing a middle C by typing a value of 261.63 is both unintuitive and impractical. There are several ways of tackling this issue within in Csound, and I’ll step you through a few in this example.

Download the source code.

The easiest way for doing twelve-tone equal temperament in Csound is to utilize the cpspch opcode, which translates a value in octave point pitch-class notation (8ve.pc) to hertz. The value for A440 in 8ve.pc is represented as 8.09. The 8 represents the octave, while the 09 is the number of half steps above the C for the specified octave. Middle C is represented as 8.00.

Another way of doing this is by specifying a formula ourselves in the code. With instr 3, users can choose a pitch by specifying the number of half-steps away from A440. For example, if p4 equals 0, the instr will sound a pitch of 440Hz. A value of -9 will sound middle C.

MIDI is a well established format that has its own way of doing things. Instrument 4 uses a modified version of instr 3’s formula, so that it accepts MIDI note value. Middle C in MIDI is 60, and entering this value will in fact sound middle C.

Here are the four formulas used in the example csd:

ifreq = p4 ; Hertz
ipch = cpspch(p4) ; cpspch
ihalf_step = 440 * 2 ^ (p4 / 12) ; Half-step (relative to A440)
imidi_note = 440 * 2 ^ ((p4 - 69) / 12) ; MIDI note

Synthesis Fall 2010

Update: Steven Yi, creator of Blue (a music composition environment for Csound) and co-editor of The Csound Journal, correctly points out that cps2pch is more accurate for tuning than cpspch. Definitely worth knowing.

[blip.tv ?posts_id=4167645&dest=-1]

Watch video at Blip.tv

Atomic Fixin’s is a boutique instrument I built with Processing and Csoundo. The synth engine is based on the principles used in the Atari 2600 video game console. I created this demo to get a sense of Csound instrument GUI design using Processing. This just happend to tie in nicely with yesterday’s post 2600 Synthesis. All in all, I would say I spent no more than 8 hours building this.

Download the source code here.

Synthesis Fall 2010

QuteCsound is the the easiest way to get up and running with Csound, with its friendly GUI and host of examples. Though it is not the only way to work with Csound. A strong alternative used by many is the command-line terminal. If you are into linux, than the terminal is probably a better match for you.

Jean-Luc wrote an article for The Csound Journal titled Working with the terminal in OSX: An absolute beginner’s guide. This will gently introduce you to the basics of using Csound from a command prompt and start to prepare you for concepts covered later in the semester, such as utilizing Csound as an audio batch processor. One note about the article, as of OS X 10.5, it is no longer necessary to add usr/local/bin to the path, rendering the second half of section II irrelevant; Csound will run in the terminal out of the box.

Synthesis Fall 2010

We’re starting off week 2 of the class with an example of a vintage synthesis technique used in the classic Atari 2600 video game console.

Download: 2600_synthesis.csd

Inside the game unit is the TIA chip which is responsible for both the graphics and the audio. Instead of trying to create a perfect emulation of the synthesis engine, we’ve narrowed today’s instruments to two defining characteristics: waveform and frequency.

The waveform is a polypulse wave, which means it looks like a pulsewave, though with multiple high and low values within a single cycle waveform. A typical polypulse looks like this:

The Atari 2600 also has a very odd tuning system that is derived from a CPU clock and and a bit shift register that stores a waveform as zeros and ones. For example, if the clock is running at 31440 Hz, and you are using a register with 15 bits, the highest frequency produced with this particular register is 2096 Hz, calculated by dividing 31440 by 15. The frequency can be modified by dividing the clock with an integer. Dividing by 2, 3 and 4 would produce frequencies of 1048, 698.666 and 524 Hz. The formula is:

frequency = sampleRate / sizeOfRegister / division

For more on Atari 2600 audio, read the ATARI 2600 VCS SOUND FREQUENCY AND WAVEFORM GUIDE by Eckhard Stolberg.

Synthesis Fall 2010

DTMF, four capital letters, printed in bold, stands for “Dual-Tone Multi-Frequency Signaling.” These are the sounds of a touch-tone telephone. And they’re quite easy to create, as they are nothing more than two sine waves of different frequencies being added together. The frequency chart is listed at Wikipedia.

You can download the Csound source code here.

I like this example for a few reasons. First and foremost, it’s simple. This is the minimal possible additive synthesizer achievable, using only two sine waves per note. DTMF tones are also a fundamental part of our telecommunications infrastructure. And this ties in perfectly with the history of computer music, since the first digital synthesizer, MUSIC, was developed at Bell Labs in 1957 by Max Mathews. Be sure to read up on Max.

Synthesis Fall 2010

Dr. Richard Boulanger, Professor of Music Synthesis at the Berklee College of Music, is the author of two beginner guides for Csound. The first is An Instrument Design TOOTorial, which gives a quick and thorough introduction to the Csound Language. The second is Introduction to Sound Design in Csound, which is practically a book in itself even though it is just the first chapter of The Csound Book.

A fact worth mentioning is that Dr. B composed the very first Csound composition, Trapped In Convert. The piece was originally written in 1979 using a music language called MUSIC 11, the precursor to Csound. In 1986, Trapped was ported to Csound. In a 2003 interview conducted by Michael Baxter, Dr. B describes what compiling music was like in those early days, “Back in 1979, it took hours to render each sound and gesture, days to render each phrase and section, and weeks to render the entire four and a half minute piece – at 24K! Today, at 44.1K, ‘Trapped in Convert’ renders in realtime on virtually any PC.”

Synthesis Fall 2010